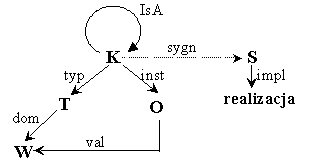
inst : K → Pfin(O)
val : O → W
Dla Grzegorza Enzo Dołęgowskiego za wpisanie moich notatek do komputera.
A - zbiór nazw atrybutów.
D - zbiór wartości atomowych (napisy, liczby, daty, wartości logiczne).
E - zbiór typów atomowych (integer, float, string, boolean, date).
K - zbiór nazw relacji (potem będzie to zbiór klas).
Nazwie relacji przyporządkowujemy skończone zbiory nazw kolumn:
kol : K → Pfin(A)
Nazwie relacji i nazwie atrybutu przyporządkowujemy typ elementarny:
typ : K × A → E
SCHrel = (K, kol, typ)
Jeśli R ∈ K, to krotka o schemacie R jest funkcją przypisującą wartości nazwom kolumn:
t : kol(R) → D
dla A ∈ kol(R), t(A) ∈ Dtyp(R,A)
W - zbiór wszystkich możliwych krotek.
Jeśli R ∈ K, to relacja o nazwie R jest skończonym zbiorem krotek o schemacie R.
Funkcja val, która przypisuje nazwom relacji egzemplarze relacji:
INSTrel = (val)
val : K → P fin(W)
SCHrel = (K, kol, typ)
INSTrel = (val)
Dla każdego R ∈ K i dla każdej krotki t ∈ val(R), t ma schemat R.
A - zbiór nazw atrybutów.
O - zbiór identyfikatorów obiektów (OID).
D - wartości atomowe (napisy, liczby, wartości logiczne).
K - zbiór nazw klas i IsA częściowy porządek na K.
E - zbiór typów atomowych (integer, float, string, boolean, date).
W to najmniejszy zbiór o następujących właściwościach:
Para (o, w) przy czym o ∈ O, w ∈ W.
T to najmniejszy zbiór o następujących właściwościach:
Relacja ≤ to częściowy porządek na T (podtyp ≤ nadtyp).
Relacja ≤ jest najmniejszym częściowym porządkiem o następujących właściwościach:
SCHstruct = (K, IsA, typ)
typ : K → T musi spełniać następujący warunek:
K IsA L ⇒ typ(K) ≤ typ(L)
Rozszerzenie bazowe to zbiór bezpośrednich obiektów klasy:
inst : K → P fin(O)
Dla każdego K, L ∈ K, K ≠ L zachodzi:
inst(K) ∩ inst(L) = ∅
Zbiór wszystkich obiektów klasy i jej podklas:
inst* : K → Pfin(O)
inst*(K) = ∪L ∈ K, L IsA K inst(L)
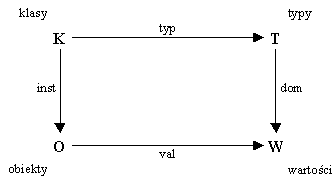
dom : T → P(W)
Jeśli SCHstruct = (K, IsA, typ) jest schematem struktury, to:
struct = (inst, val)
jest egzemplarzem schematu SCHstruct o ile spełnione są następujące warunki
inst : K → Pfin(O)
val : O → W

Niech SCHstruct = (K, IsA, typ) będzie schematem struktury.
Jeśli typ(K) jest krotkowy, to typ*(K) zawiera wszystkie składowe typ(K) oraz wszystkie A:T takie, że A:T jest składową L taką, że K IsA L i nie istnieje M różne od K i L takie, że A jest składową M i K IsA M i M IsA L.
SCHstruct jest poprawny o ile spełnione są jednocześnie oba poniższe warunki:
valst : K → Wkrotkowe
Funkcja val musi być spełniać jednocześnie oba poniższe warunki:
SCHstruct = (K, IsA, typ, valst)
Wartościowanie z wartościami domyślnymi:
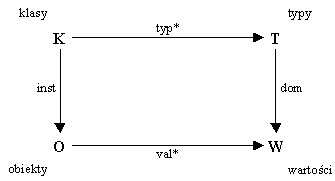
val*: O → W
val*(o) jest najuboższą wartością krotkową, która zawiera val(o) i spełnia poniższy warunek:
Jeśli:
to:
INSTstruct = (inst, val) jest egzemplarzem SCHstruct = (K, IsA, typ, valst), o ile spełnione są następujące warunki:
SCHstruct = (K, IsA, typ, valst) jest wolny od konfliktów dziedziczenia, wtw. dla każdej trójki K, L, M ∈ K takich, że M IsA K, M IsA L zachodzą następujące warunki:
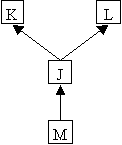
M - zbiór nazw metod.
M : K × T1 × ... × Tk → T
Przy czym M ∈ M; K ∈ K; T1, T2, ..., Tk ∈ T.
SCHzach = (K, IsA, S)
S to skończony zbiór sygnatur metod o następującej właściwości:
Jeśli (M : K × T1 × ... × Tk → T) ∈ S oraz (M : K × U1 × ... × Uk → U) ∈ S, to:
SCHzach = (K, IsA, S)
INSTzach = (inst, impl)
impl : S → Implementacje metod
impl(M : K × T1 × ... × Tk → T) = I
I to funkcja cześciowa:
I : dom(K) × dom(T1) × ... × dom(Tk) → dom(T)
Pojedyncza dyspozycja = wybór metody tylko zależy tylko pierwszego argumentu.
Wielokrotna dyspozycja = wybór metody tylko zależy od wszystkich argumentów.